Fibonacci ardıcıllığı, riyaziyyatda ən tanınan və maraqlı mövzulardan biridir. Bu ardıcıllıq yalnız riyaziyyatın əsaslarını öyrənənlər üçün deyil, həm də təbiətşünaslıq, incəsənət və iqtisadiyyat sahələrində maraqlı tətbiqlərə sahibdir. Fibonacci ardıcıllığı, riyaziyyatın təkcə abstrakt deyil, real dünyada necə müşahidə edildiyini və istifadə edildiyini göstərən güclü bir nümunədir. Bu məqalədə Fibonacci ardıcıllığının tarixi, xüsusiyyətləri, tətbiq sahələri və onun daha geniş mənada necə tətbiq olunduğu haqqında geniş məlumat verəcəyik.
Fibonacci ardıcıllığı, İtalyan riyaziyyatçısı Leonardo Fibonacci (və ya Leonardo Pisano) tərəfindən 1202-ci ildə təqdim edilmişdir. Fibonacci, Hindistan riyaziyyatından gələn və Qərb dünyasında geniş yayılmayan bəzi riyazi bilikləri Avropaya tanıtdı. “Liber Abaci” adlı əsərində, Fibonacci ardıcıllığını təqdim edərək, ədədlərin bu xüsusi ardıcıllığını izah etdi.
Fibonacci ardıcıllığının yaranma səbəbi, onun Hindistan riyaziyyatında mövcud olan bəzi tərtibatları Qərb dünyasına tanıtmaq idi. Fibonacci, “Liber Abaci” kitabında, sərhədli ticarət və iqtisadiyyat məsələləri ilə əlaqəli olaraq bu ardıcıllığı misal göstərmişdir.
Fibonacci ardıcıllığı ən sadə formada belə ifadə edilir:
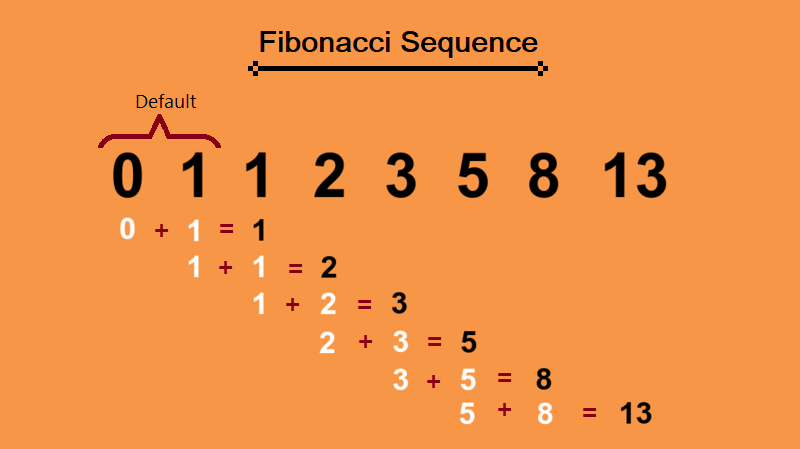
0,1,1,2,3,5,8,13,21,34,55,89,144,…
Ardıcıllığın quruluşu çox sadədir: hər bir növbəti ədəd, əvvəlki iki ədədin cəmindən yaranır.
Fibonacci ardıcıllığının hər bir növbəti ədədi əvvəlki iki ədədin cəmi olduğuna görə, bu ardıcıllıq, rekursiv bir qaydada təyin olunur. Əgər F(n) Fibonacci ardıcıllığının n-ci elementini ifadə edirsə, onda:
F(0)=0, F(1)=1, F(n)=F(n−1)+F(n−2) for n>1
Bu rekursiv quruluş, Fibonacci ardıcıllığının ən önəmli xüsusiyyətlərindən biridir. Onun tətbiqi yalnız riyaziyyatda deyil, kompüter elmlərində də geniş yayılmışdır. Fibonacci ardıcıllığı müəyyən problemləri daha səmərəli şəkildə həll etməyə kömək edir, xüsusilə də verilənlərin təkrarlanması və ardıcıl əməliyyatlar tələbi olan məsələlərdə.
Fibonacci ardıcıllığı çox maraqlı və xüsusi xüsusiyyətlərə malikdir. Bu ardıcıllığın ən mühüm xüsusiyyətlərindən biri onun təbiətdə tez-tez təkrarlanmasıdır. Fibonacci ardıcıllığının bəzi mühüm xüsusiyyətləri bunlardır:
Fibonacci ardıcıllığının ən möhtəşəm xüsusiyyətlərindən biri, ardıcıllıqda növbəti ədədlərin bir-birinə nisbətinin sabitləşməsidir. Bu nisbət çox yüksək Fibonacci ədədlərinə yaxınlaşdıqca, təqribən 1.618-ə bərabər olur. Bu sabit nisbət qızıl nisbət (və ya Φ (phi)) olaraq tanınır. Qızıl nisbət həm təbiətdə, həm də insan tərəfindən yaradılmış strukturlarda çox rast gəlinən və xüsusi simmetriya və gözəlliklə əlaqələndirilən bir ədədi nisbətdir.
limn→∞F(n+1)/F(n)=Φ≈1.618
Bu nisbət, təbiət və sənət sahələrində simmetriya və estetik mükəmməlliklə əlaqələndirilir.
Fibonacci ardıcıllığı çox vaxt təbiətdəki müxtəlif strukturlarda da özünü göstərir. Bitkilərin yarpaqlarının düzülüşü, çiçəklərin kronlarının sayı, hətta dəniz qabıqlarının spiralı, Fibonacci ardıcıllığına uyğun ola bilər. Bu təbii strukturların müxtəlif fəzalarında və quruluşlarında Fibonacci ardıcıllığının tətbiqi təbiətin təkrarlanan və ən effektiv formalarını əks etdirir.

Məsələn, bəzi çiçəklərin yarpaqları və digər təbii strukturlarda, Fibonacci ardıcıllığına əsaslanan spiral formalar müşahidə edilə bilər. Bu xüsusiyyətlər bitkilərin və heyvanların böyüməsini və inkişafını optimallaşdırır.
Fibonacci ardıcıllığının ədədləri böyüdükcə, onlar qızıl nisbətin gücləndirilmiş versiyasına yaxınlaşır. Bu xüsusiyyətin əsas tətbiqi, böyük ölçülü verilənlərin hesablanmasında daha sürətli nəticələr əldə etməkdir. Fibonacci ardıcıllığının qızıl nisbətə yaxınlaşması, təbiətdəki və insanlar tərəfindən yaradılan strukturlarda yüksək səmərəlilik və optimallıq nəzərə çarpır.
Fibonacci ardıcıllığı yalnız riyaziyyatın və təbiətin sahələrində deyil, bir çox başqa sahələrdə də geniş şəkildə istifadə olunur. Bu ardıcıllığın tətbiqləri çox genişdir və aşağıda ən əsas sahələrdən bəzilərini təqdim edirik.
Fibonacci ardıcıllığı, riyaziyyatda çoxsaylı modellərin qurulmasında istifadə edilir. Məsələn, ardıcıllığın rekursiv təbiəti, komputer alqoritmlərinin təkmilləşdirilməsi və verilənlərin analizində istifadə olunur. Fibonacci ardıcıllığı, həmçinin qraf nəzəriyyəsində və şəbəkə nəzəriyyəsində müxtəlif problemləri həll etmək üçün istifadə olunur.
Fibonacci ardıcıllığı təbiətdə çox vaxt qarşımıza çıxır. Məsələn, bəzi bitkilərin yarpaqları, çiçəkləri və meyvələrinin düzümləri Fibonacci ardıcıllığına uyğun olur. Həmçinin, bəzi heyvanların bədənində və qabıqlarında da bu ardıcıllıq müşahidə edilə bilər. Təbiətin inkişaf proseslərində və bəzi bioloji formaların qurulmasında Fibonacci ardıcıllığının rolu əvəzolunmazdır.
Fibonacci ardıcıllığının qızıl nisbəti, sənət və memarlıq sahələrində də geniş istifadə edilir. Təbiətdəki mükəmməl simmetrik strukturların tərtibində bu nisbət, estetik gözəllik və harmoniya yaratmaq məqsədilə istifadə olunur. Məşhur memar və sənətkarlar, qızıl nisbəti işlərində istifadə edərək, mükəmməl estetik nəticələr əldə ediblər.
Fibonacci ardıcıllığı iqtisadiyyatda da istifadə olunur. Məsələn, maliyyə bazarlarında qiymətlərin dəyişmə trendinin proqnozlaşdırılması və müvafiq ticarət strategiyalarının qurulmasında Fibonacci nisbətləri əsas alınır. Fibonacci ardıcıllığına əsaslanan alqoritmlər və modellər, bazar hərəkətlərini təhlil edərək, gələcəkdəki qiymət dəyişikliklərini proqnozlaşdırmağa kömək edir.
Fibonacci ardıcıllığı və onun təbii və riyazi xüsusiyyətləri çox geniş və maraqlı bir mövzudur. Bu ardıcıllığın tarixi, xüsusiyyətləri və tətbiqləri riyaziyyatdan təbiətə, sənətə və iqtisadiyyata qədər bir çox sahədə əhəmiyyət kəsb edir. Fibonacci ardıcıllığı yalnız riyaziyyatın sadə bir nümunəsi deyil, həm də təbiətin quruluşunu və estetik simmetriyasını anlamağımıza kömək edən bir vasitədir. Onun tətbiqləri gələcəkdə daha da genişlənə bilər, çünki bu ardıcıllıq təbiət və cəmiyyətin müxtəlif sahələrində mühüm bir rol oynayır.
